| Projecto POLYA |
||
Resolução
do problema

|
||
|
Inicialmente, aponto todas as informações importantes sobre o problema:

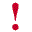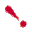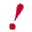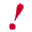
 Como estes 4 algarismos vamos constituir um número: milhares centenas dezenas unidades
Para resolver este pequeno enigmas temos que conhecer bem os números pares. Eu sei que para um número ser par a algarismo das unidades também tem que ser par. O que nos indica que o 5 não pode ocupar a posição das unidades. Assim, sobram os algarismos 4, 6 e 8 para ocupar a posição das unidades. 
Por enquanto não consigo concluir mais nada
sobre o algarismo que deve ocupar
as unidades, por isso vou tentar descobrir qual é o
número mais indicado para eu colocar na posição
dos milhares de forma a obter o menor número
possível.
Pensando um bocadinho percebo que, para ter o menor número possível, o algarismo dos milhares tem também que ser o mais pequeno possível. Dos números que podemos usar, 4 é o mais pequeno. Então o 4 tem que ocupar a posição dos milhares. 4 centenas dezenas unidades 5, 6 ou 8 5, 6 ou 8 6 ou 8 Seguindo o mesmo raciocínio, descubro que o ideal é colocar nas centenas o número mais pequeno de entre as possibilidades. As possibilidades são 5, 6 ou 8, logo o menor número é 5. Ou seja, ficamos com: 4 5 dezenas unidades 6 ou 8 6 ou 8 Se escolhermos o 6 para as dezenas e o 8 para as unidades fica: 4 5 6 8 Se escolhermos o 8 para as dezenas e o 6 para as unidades fica: 4 5 8 6 O menos dos dois é 4 5 6 8, o que vai de encontro ao raciocínio que segui até agora.
Para obter o menor número par começei por excluir os algarismos que não são pares para a casa das unidades. Depois verifiquei que os algarismo mais pequenos teriam que estar sempre nas casas maiores (primeiro nos milhares, depois nas centenas, posteriormente nas dezenas e, só por último, nas unidades). A solução
que o Tó teve que encontrar é:
    |
||
|
|
||


