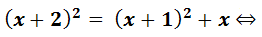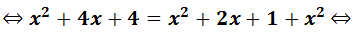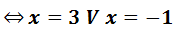Projecto POLYA



Resolução do problema

A cerca do quintal...     

1º...   Analiso as condições do enunciado.

O senhor Francisco pretende construir uma cerca para o quintal que tem a forma de um triângulo rectângulo.

As dimensões do quintal são três números inteiros consecutivos.

O senhor Francisco comprou 10 m de rede para fazer a cerca.
                                                                                                                                                
2º...   Faço um esquema, identificando os dados e a incógnita                                                                  





3º...  Traduzo o enunciado por uma equação                                                                             

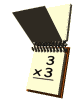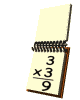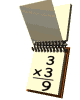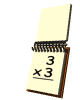Utilizando o Teorema de Pitágoras tem-se:

4º...  Resolvo a equação





 Equação completa do 2º grau
Usando a fórmula resolvente tem-se:







4º...  Analiso as soluções da equação

A solução x = -1 não pode ser comprimento do lado do triângulo uma vez que não existem comprimentos negativos.
Deste modo x = 3 é a solução do problema.
Sendo assim os lados do quintal do senhor Francisco medem 3m, 4m e 5m.
5º...  Comparo o perímetro do quintal com a quantidade de rede que o senhor Francisco comprou                    

O perímetro de um polígono é a soma do comprimento de todos os lados, portanto: P= l+l+l

Sendo assim,    P= 3 + 4 + 5
                    P= 12 m

O perímetro do quintal é 12 metros, logo os 10 metros de rede que o senhor Francisco comprou não chegam para o vedar!

 
Página de enunciados