|
Projecto POLYA
|
|
|
|
|
|
Resolução
do problema |
|
|
Onde
foi o assalto?

|
|
|
 1º...
Verifico o que quero descobrir...
1º...
Verifico o que quero descobrir...
Pretendo descobrir o local do
assalto!
|
|
|
2º...
Analiso os dados do enunciado...
|
|
|
- O assalto deu-se na cidade do sol,
a mais de 2km da esquadra.
- O ponto da cidade mais afastado da esquadra
está a 6km.
- Existem duas ruas,entre a esquadra e o exterior da
cidade.
- Há três locais possíveis para o
crime.
|
|
|
3º... Analiso as condições que os
dados devem satisfazer...
|
|
|
- O local do assalto é a
mais de 2km da esquadra.
- Da esquadra à ponta mais afastada da cidade
são 6km.
- As duas ruas que dão acesso ao exterior da
cidade intersectam-se na esquadra e são perpendiculares entre si.
- A rua do crime une as duas saídas da cidade.
- O local do crime fica equidistante
dos extremos da rua.
|
|
|
4º... Planeio a estratégia de
resolução...
Este problema,
parece ser um problema geométrico, por isso vou utilizar um
esquema. Neste esquema vou construir com régua e compasso os
lugares geométricos que satisfazem as condições do
enunciado.
|
|
|
|
|
|
5º... Executo a estratégia de
resolução...
|
|
|
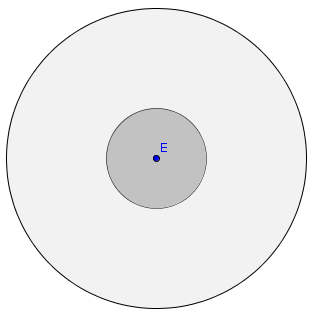
| O local do assalto é a
mais de 2km da esquadra. |
 |
Marco
um ponto que represente a esquadra. Com centro neste ponto e raio
correspondente a 2km, por exemplo 2cm, desenho uma circunferencia. |
 |
|
 |
| Da
esquadra à ponta mais afastada da cidade são 6km. |
 |
A
ponta mais afastada da cidade fica a 6km da esquadra, logo a cidade
fica no interior de uma circunferencia de centro na esquadra e raio 6km. |
 |
|
 |
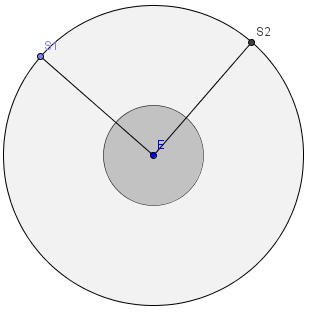
| As
duas ruas que dão acesso ao exterior da cidade intersectam-se na
esquadra e são perpendiculares entre si. |
 |
Escolho um ponto (S1) da circunferencia,
para ser uma saída da cidade. Traço um segmento de recta ([ES1]) entre esse ponto e a esquadra.
Pelo ponto E traço um segmento perpendicular a [ES1]. |
 |
|
 |
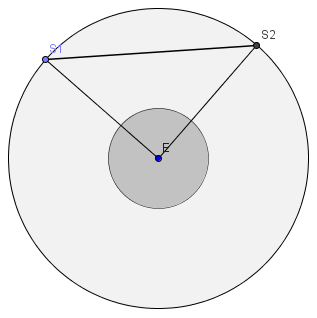
| A rua do crime une as
duas saídas da cidade. |
 |
Traço o
segmento ([S1S2]). |
 |
|
 |
| O local do crime fica
equidistante dos extremos da rua. |
 |
Para saber o local do crime resta marcar
o ponto equidistante de S1 e S2, ou seja o ponto médio do
segmento ([S1S2]). |
 |
|
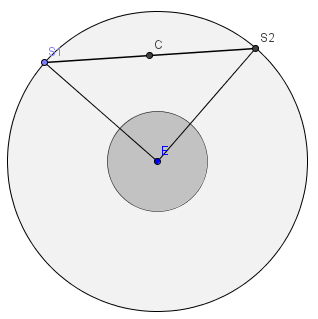 |
O ponto equidistante das
duas saídas da cidade é o ponto C.
|
|
|
|
|
|
6º... Verifico a solução...
|
|
|
 |
Observando a construção
verifico que C respeita todas as condições exigidas:
C é o ponto médio
da rua que liga as duas
saídas da cidade. Estas saídas pertencem a duas ruas
perpendiculares em E.
C está a mais de 2km e a menos de 6km da esquadra.
|
|
|
|
Desta
forma C é o local do crime. |
|
|
|
|
|
Página de enunciados
|
|














