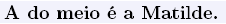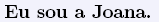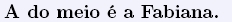Projecto POLYA




Resolução do problema

Quem é quem?!   

1º...


Verifico que tenho três raparigas, que estão mascaradas. Pretendo descobrir qual delas está mascarada de quê.
Não posso é esquecer que uma delas mente sempre, outra fala sempre verdade e outra umas vezes mente outras vezes diz a verdade.


2º...

Considero que uma delas, por exemplo a rapariga A é a Matilde e fala verdade. Tendo em conta a verdade ou falsidade da afirmação de A, decido a verdade ou falsidade das outras.
Caso não consiga concluir nada, considero que outra das raparigas fala verdade e procedo da mesma forma.

3º...






A= Matilde   »» B=Matilde
C
Mentira, mas Matilde nunca mente.




Se A for a Matilde, então está a dizer que a rapariga do meio, ou seja a B é a Matilde. Nesta caso a Matilde está a mentir, então A não é a Matilde.






A
B=Matilde
C


Mentira, porque B diz que é a  Joana.


Se B for a Matilde, então está a mentir porque diz que é a Joana e tal não pode acontecer.






A=Joana
B=Fabiana
C=Matilde
Sendo B a Fabiana, C a Matilde, tem-se que a rapariga A é a Joana. «« Como a Matilde fala  verdade, a rapariga B é a Fabiana.
 «« Por exclusão de partes, a rapariga C é a Matilde, logo fala sempre verdade.

A rapariga C é a Matilde. Pela sua afirmação a rapariga B é a Fabiana e portanto a rapariga A é a Joana.


Posso então concluir que a Joana está mascarada de pantera cor de rosa, a Fabiana está mascarada de índia e a Matilde de diabinha.




Página de enunciados